Systemy liczbowe i warunki

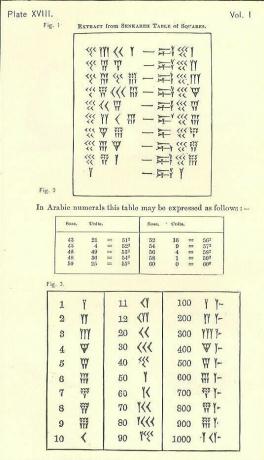
Trzy główne obszary różniące się od naszych liczb

Wyobraź sobie, o ile łatwiej byłoby nauczyć się arytmetyki we wczesnych latach, gdyby wszystko, co musiałeś zrobić, to nauczyć się pisać linię taką jak ja i trójkąt. To właściwie wszystko, co musieli zrobić starożytni mieszkańcy Mezopotamii, chociaż zróżnicowali ich tu i tam, wydłużając, obracając itp.

Nie mieli naszych piór i ołówków ani papieru. To, co napisali, było narzędziem używanym w rzeźbie, ponieważ medium było gliną. Niezależnie od tego, czy jest to trudniejsze, czy łatwiejsze do nauczenia się obsługi niż ołówek, jest to rzut losowy, ale jak dotąd są one wyprzedzane w dziale łatwości, mając tylko dwa podstawowe symbole do nauczenia się.

Następny krok wrzuca klucz do działu prostoty. Używamy Baza 10, koncepcja wydaje się oczywista, ponieważ mamy 10 cyfr. Właściwie mamy 20, ale załóżmy, że mamy sandały z ochronnymi palcami, które chronią przed piaskiem pustynię, gorącą od tego samego słońca, która upiekłaby gliniane tabliczki i zachowała je dla nas przez tysiące lat później. Babilończycy wykorzystali tę Bazę 10, ale tylko częściowo. Częściowo użyli bazy 60, tej samej liczby, którą widzimy wokół nas w minutach, sekundach i stopniach trójkąta lub koła. Byli znakomitymi astronomami, więc liczba mogła pochodzić z ich obserwacji nieba. Baza 60 zawiera również różne przydatne czynniki, które ułatwiają obliczanie. Jednak nauka bazy 60 jest zastraszająca.

W „Homage to Babylonia” [The Mathematical GazetteVol. 76, nr 475, „Wykorzystanie historii matematyki w nauczaniu matematyki” (mar., 1992), ss. 158-178], pisarz-nauczyciel Nick Mackinnon mówi, że używa babilońskiej matematyki do nauczania 13-latków o podstawach innych niż 10. System babiloński używa podstawy-60, co oznacza, że ​​zamiast dziesiętnego, jest płciowy.

Zarówno babiloński system liczbowy, jak i nasz, polegają na pozycji, aby dać wartość. Oba systemy robią to inaczej, częściowo dlatego, że w ich systemie brakowało zera. Nauka babilońskiego systemu od lewej do prawej (od wysokiej do niskiej) dla pierwszego smaku podstawowej arytmetyki prawdopodobnie już nie jest trudne niż nauka naszego dwukierunkowego, w którym musimy pamiętać kolejność liczb dziesiętnych - rosnących od dziesiętnych, jedności, dziesiątki, setki, a potem wachlowanie w przeciwnym kierunku po drugiej stronie, bez kolumny oneths, tylko dziesiąte, setne, tysięczne itp.

Przejdę do pozycji systemu babilońskiego na dalszych stronach, ale najpierw trzeba nauczyć się kilku ważnych liczb.

Mówimy o okresach lat przy użyciu liczb dziesiętnych. Mamy dekadę na 10 lat, stulecie na 100 lat (10 dekad) lub 10X10 = 10 lat do kwadratu i tysiąclecie na 1000 lat (10 stuleci) lub 10X100 = 10 lat sześciennych. Nie znam żadnego wyższego terminu, ale nie są to jednostki używane przez Babilończyków. Nick Mackinnon odnosi się do tabletki od Senkareh (Larsa) od Sir Henry'ego Rawlinsona (1810–1895) * dla jednostek używanych przez Babilończyków, nie tylko dla zaangażowanych lat, ale także sugerowanych ilości:

1. soss
2. ner
3. sar.

sossnersosssarsoss

Nadal nie ma szans na rozstrzygnięcie: niekoniecznie łatwiej jest nauczyć się pochodnych wyrażonych w kwadratach i sześcianach z łaciny niż sylaby babilońskie, które nie wymagają dzielenia, ale pomnożenie przez 10.

Co myślisz? Czy trudniej byłoby nauczyć się podstaw liczb jako babilońskie dziecko w szkole czy jako nowoczesny uczeń w anglojęzycznej szkole?

* George Rawlinson (1812-1902), brat Henry'ego, pokazuje uproszczoną tabelę kwadratów w transkrypcji Siedem wielkich monarchii starożytnego świata wschodniego. Tabela wydaje się astronomiczna, oparta na kategoriach lat babilońskich.

Wszystkie zdjęcia pochodzą z tej zeskanowanej online wersji XIX-wiecznego wydania George'a Rawlinsona Siedem wielkich monarchii starożytnego świata wschodniego.

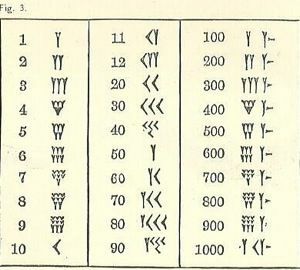
Ponieważ dorastaliśmy z innym systemem, liczby babilońskie są mylące.

Przynajmniej liczby biegną od wysokich po lewej do niskich po prawej, podobnie jak nasz system arabski, ale reszta będzie prawdopodobnie wydawać się nieznana. Symbolem jednego jest klin lub forma w kształcie litery Y. Niestety, Y reprezentuje również 50. Istnieje kilka osobnych symboli (wszystkie oparte na klinie i linii), ale wszystkie inne liczby są z nich utworzone.

Pamiętaj, że forma pisania jest klinowy lub w kształcie klina. Ze względu na narzędzie używane do rysowania linii istnieje niewielka różnorodność. Klin może, ale nie musi, mieć ogon, narysowany przez pociągnięcie rysika pisma klinowego wzdłuż gliny po nadrukowaniu części trójkąta.

Cyfra 10, opisana jako grot strzałki, wygląda trochę jak

Trzy rzędy, do 3 małych 1s (napisane jak Ys z kilkoma skróconymi ogonami) lub 10s (10 jest napisane jak

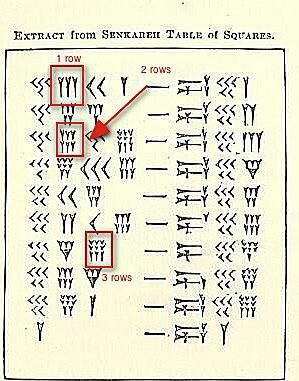
Istnieją trzy zestawy liczb klinowych klastry wyróżnione na powyższej ilustracji.

W tej chwili nie interesuje nas ich wartość, ale pokazanie, jak zobaczysz (lub napiszesz) gdziekolwiek od 4 do 9 tego samego numeru zgrupowanych razem. Trzej idą z rzędu. Jeśli jest czwarty, piąty lub szósty, idzie poniżej. Jeśli jest siódmy, ósmy lub dziewiąty, potrzebujesz trzeciego rzędu.

Kolejne strony zawierają instrukcje wykonywania obliczeń z klinem babilońskim.

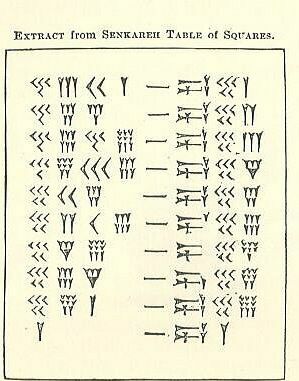
Z tego, co przeczytałeś powyżej na temat soss - który zapamiętasz jako babiloński przez 60 lat, klin i grot strzały - które są opisowymi nazwami znaków klinowych, sprawdź, czy możesz dowiedzieć się, jak działają te obliczenia. Jedna strona znaku przypominającego myślnik to liczba, a druga to kwadrat. Wypróbuj jako grupa. Jeśli nie możesz tego rozgryźć, spójrz na następny krok.

Czy potrafisz to teraz rozgryźć? Daj temu szansę.

...

Po lewej stronie znajdują się 4 jasne kolumny, po których następuje znak podobny do myślnika i 3 kolumny po prawej stronie. Patrząc na lewą stronę, odpowiednikiem kolumny 1s są w rzeczywistości 2 kolumny najbliższe „myślnikowi” (kolumny wewnętrzne). Pozostałe 2 zewnętrzne kolumny są liczone razem jako kolumna z lat 60.

• 4-
• 3-Ys = 3.
• 40+3=43.
• Jedynym problemem jest to, że jest po nich kolejny numer. Oznacza to, że nie są to jednostki (miejsce tych). 43 nie jest 43-jedynkami, ale 43-60, ponieważ jest to system płciowy (baza-60) i jest w soss kolumna, jak wskazuje dolna tabela.
• Pomnóż 43 przez 60, aby uzyskać 2580.
• Dodaj kolejny numer (2-
• Masz teraz 2601.
• To jest kwadrat 51.

Następny wiersz ma 45 w soss kolumna, więc pomnożymy 45 przez 60 (lub 2700), a następnie dodajesz 4 z kolumny jednostek, więc masz 2704. Pierwiastek kwadratowy z 2704 wynosi 52.

Czy potrafisz zrozumieć, dlaczego ostatnia liczba = 3600 (60 do kwadratu)? Wskazówka: Dlaczego nie jest to 3000?